三角関数とは？基本公式とグラフを教え方と合わせて徹底解説｜高校数学

高校数学における三角関数の基本は、単位円をベースに考えていくことです。高校生に教える際のポイントを、基本公式からやさしく解説します。

なお、次の単元の基本的な解き方については、以下の記事をご覧ください。

・三角方程式・三角不等式

・加法定理・倍角の公式・半角の公式・3倍角の公式

・和積公式・合成

解き方・教え方がわかる事典｜中学・高校数学

三角比の基本

三角比とは

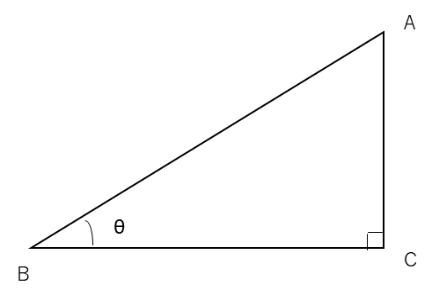
直角三角形ＡＢＣの∠ＡＢＣ＝Θとすると、

ｓｉｎΘ＝ＡＣ／ＡＢ……Θの正弦

ｃｏｓΘ＝ＢＣ／ＡＢ……Θの余弦

ｔａｎΘ＝ＡＣ／ＢＣ……Θの正接

ー１≦ｓｉｎΘ≦１、ー１≦ｃｏｓΘ≦１、ｔａｎΘは実数全体

また、基本公式は以下の3つです。

ｓｉｎ²Θ＋ｃｏｓ^2Θ＝１

ｔａｎΘ＝ｓｉｎΘ／ｃｏｓΘ

１＋ｔａｎ²Θ＝１／ｃｏｓ²Θ

例題

①ｓｉｎΘ＝２／３のとき、ｃｏｓΘとｔａｎΘの値を求めよ。

②ｔａｎΘ＝２のとき、ｓｉｎΘとｃｏｓΘの値を求めよ。

③ｓｉｎΘーｃｏｓΘ＝１／２のとき、ｓｉｎΘｃｏｓΘの値を求めよ。

〈解答〉

いずれの問題も、三角関数の基本公式を使って解きます。

①

ｓｉｎ²Θ＋ｃｏｓ^2Θ＝１にｓｉｎΘ＝２／３を代入すると、

（２／３）²＋ｃｏｓ²Θ＝１

ｃｏｓ²Θ＝５／９

ｃｏｓΘ＝±√５／３

ｔａｎΘ＝ｓｉｎΘ／ｃｏｓΘにｓｉｎΘ＝２／３・ｃｏｓΘ＝±√５／３を代入すると、

ｔａｎΘ＝±２√５／５

②

１＋ｔａｎ²Θ＝１／ｃｏｓ²ΘにｔａｎΘ＝２を代入すると、

１＋２²＝１／ｃｏｓ²Θ

ｃｏｓ²Θ＝１／５

ｃｏｓΘ＝±√５／５

ｓｉｎ²Θ＋ｃｏｓ^2Θ＝１にｃｏｓΘ＝±√５／５を代入すると、

ｓｉｎ²Θ＝４／５

ｓｉｎΘ＝±２√５／５

③

ｓｉｎΘーｃｏｓΘ＝１／２

（ｓｉｎΘーｃｏｓΘ）²＝（１／２）²

ｓｉｎ²Θー２ｓｉｎΘｃｏｓΘ＋ｃｏｓ²Θ＝１／４

ｓｉｎ²Θ＋ｃｏｓ^2Θ＝１を代入すると、

１ー２ｓｉｎΘｃｏｓΘ＝１／４

ｓｉｎΘｃｏｓΘ＝３／８

単位円を使って三角関数の性質を押さえる

ーΘの三角関数

ｓｉｎ（ーΘ）＝ーｓｉｎΘ

ｃｏｓ（ーΘ）＝ｃｏｓΘ

ｔａｎ（ーΘ）＝ーｔａｎΘ

なぜ上記の等式が成り立つのか、単位円を書いて確認してみましょう。

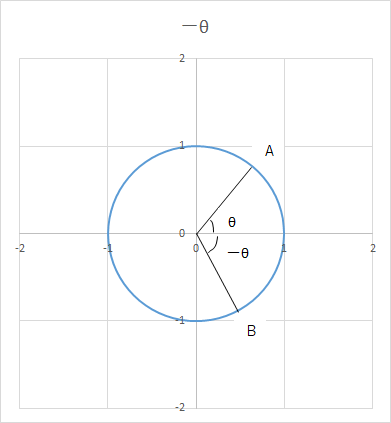
上図において、単位円上の点Ａ・Ｂはｘ軸に関して対称であるので、Ａ（Ｘ、Ｙ）・Ｂ（Ｘ、ーＹ）とおける。

ＡＯ＝ＢＯ＝１であるから、

ｓｉｎΘ＝Ａのｙ座標／ＡＯ＝Ｙ……①

ｃｏｓΘ＝Ａのｘ座標／ＡＯ＝Ｘ……②

ｔａｎΘ＝Ａのｙ座標／Ａのｘ座標＝Ｙ／Ｘ……③

ｓｉｎ（ーΘ）＝Ｂのｙ座標／ＢＯ＝ーＹ＝ーｓｉｎΘ（∵①）

ｃｏｓ（ーΘ）＝Ｂのｘ座標／ＢＯ＝Ｘ＝ｃｏｓΘ（∵②）

ｔａｎ（ーΘ）＝Ｂのｙ座標／Ｂのｘ座標＝ーＹ／Ｘ＝ーｔａｎΘ（∵③）

Θ＋π／２（90°）の三角関数

ｓｉｎ（Θ＋π／２）＝ｃｏｓΘ

ｃｏｓ（Θ＋π／２）＝ーｓｉｎΘ

ｔａｎ（Θ＋π／２）＝ー１／ｔａｎΘ

なぜ上記の等式が成り立つのか、単位円を書いて確認してみましょう。

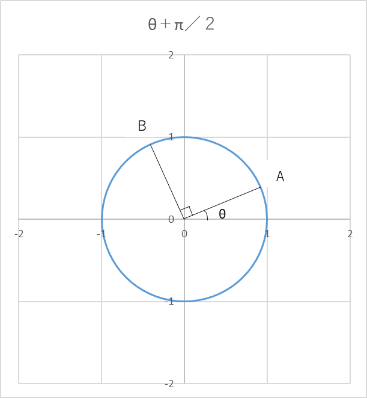
上図のように単位円上に点Ａ・Ｂをとる。点Ａ（Ｘ、Ｙ）とおくと、点Ｂ（ーＹ、Ｘ）とおける。

ｓｉｎ（Θ＋π／２）＝Ｂのｙ座標／ＢＯ＝Ｘ＝ｃｏｓΘ（∵②）

ｃｏｓ（Θ＋π／２）＝Ｂのｘ座標／ＢＯ＝ーＹ＝ーｓｉｎΘ（∵①）

ｔａｎ（Θ＋π／２）＝Ｂのｙ座標／Ｂのｘ座標＝ーＸ／Ｙ＝ー１／ｔａｎΘ（∵③）

Θ＋π（180°）の三角関数

ｓｉｎ（Θ＋π）＝ーｓｉｎΘ

ｃｏｓ（Θ＋π）＝ーｃｏｓΘ

ｔａｎ（Θ＋π）＝ｔａｎΘ

なぜ上記の等式が成り立つのか、単位円を書いて確認してみましょう。

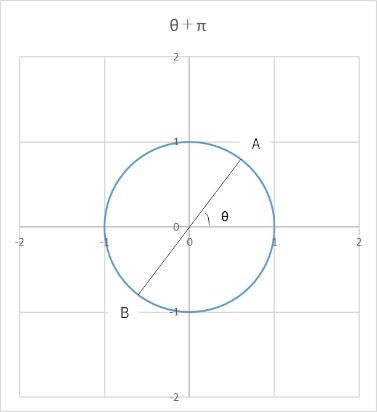
上図のように単位円上に点Ａ・Ｂをとる。点Ａ（Ｘ、Ｙ）とおくと、点Ｂ（ーＸ、ーＹ）とおける。

ｓｉｎ（Θ＋π）＝Ｂのｙ座標／ＢＯ＝ーＹ＝ーｓｉｎΘ（∵①）

ｃｏｓ（Θ＋π）＝Ｂのｘ座標／ＢＯ＝ーＸ＝ーｃｏｓΘ（∵②）

ｔａｎ（Θ＋π）＝Ｂのｙ座標／Ｂのｘ座標＝Ｙ／Ｘ＝ｔａｎΘ（∵③）

例題

①ｓｉｎ７／２ π

②ｃｏｓ(ー４／３ π)

〈解答〉

①２πで単位円を1周して元に戻ることから、

ｓｉｎ７／２ π＝ｓｉｎ（３／２ π＋２π）＝ｓｉｎ３／２ π

＝ｓｉｎ（１／２ π＋π）＝ーｓｉｎ１／２ π

＝－１

②ｃｏｓ（ー４／３ π）＝ｃｏｓ４／３ π

＝ｃｏｓ（１／３ π＋π）＝ーｃｏｓ１／３ π

＝ー１／２

三角関数のグラフとは

ｙ＝ｓｉｎΘのグラフ

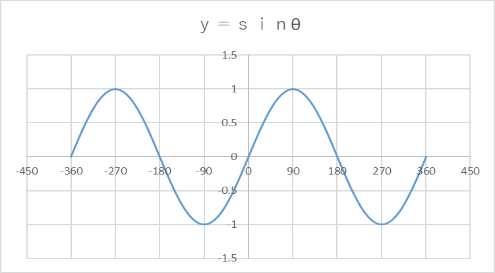
Θは実数全体をとり、－１≦ｙ≦１です。また、周期は２π（360°）です。

ｙ＝ｃｏｓΘのグラフ

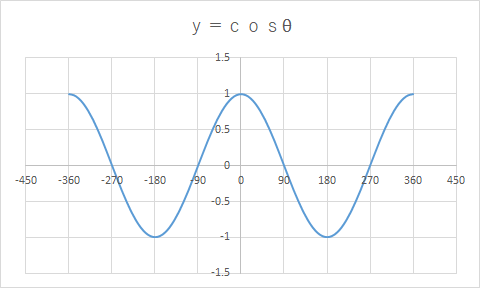
Θは実数全体をとり、－１≦ｙ≦１です。また、周期は２π（360°）です。

ｓｉｎΘが原点スタートで、ｃｏｓΘは点（０、１）スタートだと覚えておきましょう。

ｙ＝ｔａｎΘのグラフ

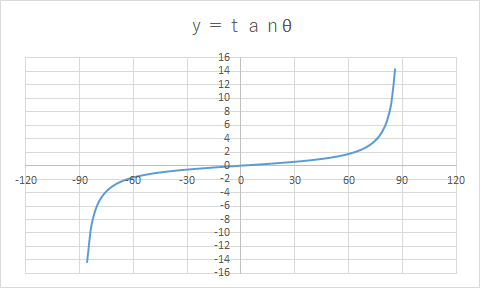
Θ＝ー90°・90°に限りなく近づいていくというイメージです。直線Θ＝π／２＋ｋπ（ｋは整数）が漸近線です。

ｙはすべての実数をとりますが、Θ≠π／２＋ｋπ（ｋは整数）となります。なお、周期はπ（180°）です。

グラフの平行移動・拡大・縮小

グラフの平行移動については、一次関数のグラフの考え方と同じです。

ｙ＝ｆ(ｘ)のグラフを、ｘ軸方向にｐ、ｙ軸方向にｑだけ平行移動すると、ｙ＝ｆ(ｘーｐ)＋ｑとなります。

例えば、ｙ＝ｓｉｎ（Θーπ／３）のグラフは、ｙ＝ｓｉｎΘのグラフをΘ軸方向にπ／３平行移動したものです。周期は２πのまま変わりません。

グラフの拡大・縮小については、ｘ軸方向とｙ軸方向の2種類があります。

ｙ＝ｆ(ｘ)のグラフをｙ軸方向にｋ（ｋ＞０）倍すると、ｙ＝ｋｆ(ｘ)となります。

例えば、ｙ＝１／２ｃｏｓΘのグラフは、ｙ＝ｃｏｓΘのグラフをｙ軸方向に１／２倍に縮小したものになります。周期は２πのまま変わりません。

ｙ＝ｆ(ｘ)のグラフをｘ軸方向に１／ｋ（ｋ＞０）倍すると、ｙ＝ｆ(ｋｘ)となります。逆数になることに注意しましょう。

例えば、ｙ＝ｓｉｎΘ／２は、ｙ＝ｓｉｎΘのグラフをΘ軸方向に２倍に拡大したものになります。周期は２π÷１／２＝４πです。

三角関数の基本とグラフを教えるポイント

基本事項を理解しているかを確認しよう

慣れが勝負です。簡単めの問題を多めに解いて、基本事項を確実に理解しましょう。

また、既習範囲である三角比の確認もしてください。

単位円とグラフを何度も書く！

ｓｉｎ(Θ＋π／２)やｃｏｓ(Θ＋π)がｓｉｎΘやｃｏｓΘとどのように異なるかを直感的に理解するのは簡単ではありません。

単位円をしっかりと書いて考えましょう。

グラフは、Θ軸が０、π／２、π、３／２π、２πあたりが基準です。

平行移動・拡大・縮小のパターンをしっかり理解しましょう！

慣れないうちは、簡単な求値問題であっても、単位円やグラフを書く癖をつけるのがオススメです。

図をきちんと書くよう、お子さんに繰り返し伝えてあげてください。

概要が理解できれば問題演習を重ねよう

教えてもらっている状態で問題が解けたとしても、独力でできなければ意味がありません。分かった気になっているだけ、ということもあります。

思考力が問われる数学であっても、反復練習は非常に大事です。簡単な問題から標準レベルの問題まで、段階を踏んで解いていくようにしましょう。

解けた問題には○、解けなかった問題には△や×をつけ、2周目以降では△や×の問題を中心にやり直すようにしてください。

今回解説した範囲は、三角関数の標準～応用問題を解くために必須の内容です。焦らず、時間をかけて基礎の土台をつくりましょう。

オススメの問題集は、『新課程　チャート式　基礎と演習数学I+A』（数研出版）や『新課程　チャート式　基礎からの数学I+A』（数研出版）です。

前者の方が問題は易しめです。

お子さんの理解が進まないパターン3選とその対処法

教えてもなかなか理解してもらえない

根気よく何度も例題レベルの問題を一緒に解いてください。

ヒントを出しながら解いてもらい、徐々にヒントの量を減らすというのも有効です。

なお、グラフの平行移動・拡大・縮小については、結果を暗記するというやり方でも問題ありません。

教えるとその場ではできるのに、お子さん一人で問題を解くと間違いが多発

このパターンは、さらに以下の2パターンに大別できます。

①問題演習が足りていない

→問題演習で基礎レベルから順番に解いていきましょう。

②教えられた時は分かった気になっている

→どこでつまずいているのかを分析、理解できていないポイントを再説明しましょう。その後、説明したポイントが理解できているかを測れる問題を演習できるとベストです。

単位円やグラフを正しく書けるかどうかがポイントです。

様々なパターンの問題に触れ、とにかく手を動かしてもらいましょう！

教えようとすると、ちょっとした間違いを指摘しただけで機嫌が悪くなり、うまくいかない

思春期で親子関係が難しく、接し方にデリケートな配慮が必要な場合があります。

1つ指摘するときは1つ以上ほめることを意識しましょう。ほめる内容は、学習を着実に進められている点などにするのがオススメです。

そして大事なことは、「根気強く、粘り強く」です。保護者の方が不機嫌になったり、イライラしたりしないように心がけてください。

子どもに教えるというのは、なかなかにストレスが溜まる作業です。保護者の方の息抜きも必要でしょう。根を詰めてやりすぎると、保護者の方もお子さんもしんどくなってしまいます。

教えるのが大変……。成績低迷に悩む中高一貫校生なら、専門塾WAYSで92.9％が成績アップ！

最後に、お子さんが中高一貫校生で、成績低迷に悩んでいるのであれば、「中高一貫校専門 個別指導塾WAYS」をおすすめします。

• 思春期で親子関係が難しくなってきた
• 子どもの勉強を見る時間がなかなか取れない
• 勉強の内容が難しくなり、教えられなくなってきた

以上のように、家庭でのサポートが難しい場合にも、学習塾の活用は理にかなっています。

500校以上の指導ノウハウ＆9割以上の成績アップ実績

WAYSは、成績が低迷してしまっている中高一貫校生の、授業・定期テストのサポートに特化した、補習塾タイプの個別指導塾です。

一番の強みは、500校以上の中高一貫校生を指導してきたノウハウと、9割以上の塾生の成績を跳ね上げてきた実績です。

確認テストの実施や、生徒に問題を解説してもらうなどの指導スタイルで、塾生は確実に理解を深めていきます。