【応用編】一次関数のグラフの変域と文章題とは？ポイントと教え方を解説｜中学数学

一次関数におけるグラフの変域と文章題について、中学生に教える際のポイントを基礎からやさしく解説します。一次関数の応用編です。

解き方・教え方がわかる事典｜中学・高校数学

一次関数の変域とは

一次関数は一本の直線ですので、ｘはどのような値にもなり、また、ｙもそれに応じてどのようにも変化します。

そのなかで、ｘやｙのとれる範囲を限定するというのが、変域の考え方です。無限に伸びる一本の直線の一部を切り取るイメージですね。

変域は、「変数のとれる値の範囲」という意味です。ｘの変域を定義域、ｙの変域を値域といいます。

例えば、一次関数ｙ＝ｘ＋２において、定義域が１≦ｘ≦４のとき、値域は３≦ｙ≦６となります。

また、ｙ＝ーｘ＋２において、定義域が１≦ｘ≦４のとき、値域は－２≦ｙ≦１となります。

一次関数の文章題とは

一定の割合で水を入れる、一定の速度で移動するなど、一定の割合で物事を続けるという設定の場合、一次関数を用いることができます。

日本語の文章をｙ＝ａｘ＋ｂに置き換えましょう。

例えば、4Ｌの水が入っているところに、毎分3Ｌずつ水を入れるとき、ｘ分後の水の量ｙＬは、ｙ＝３ｘ＋４と表せます。

さらに、19Ｌまでしか入らない水槽という設定であれば、5分後には水槽は満杯になります。

ということは、定義域は0≦ｘ≦5（時間はマイナスにならない）、値域は4≦ｙ≦19となります。

一次関数の変域を教えるポイント

まずは適当な直線の式を図示し、直線が無限に伸びることを確認します。

例えば、ｙ＝－２ｘ＋４のグラフを描画してみてください。

ここでは仮に、定義域が－２≦ｘ＜３であるとします。値域は－２＜ｙ≦８となります。

このとき、グラフ上では、変域内（－２≦ｘ＜３）の部分を実線、それ以外の部分を破線にするのが一般的です。

そして、実線と破線の境目の座標については、「≦」のように端の点を含む場合は黒丸、「＜」のように端の点を含まない場合は白丸とします。

上記の例では、点（３、－２）は含まないので白丸、点（－２、８）は含むので黒丸としましょう。

合わせて、「変数のとれる値の範囲」のことを変域といい、ｘの変域を定義域、ｙの変域を値域と呼ぶことを伝えてください。

その他、様々な直線の式を用いて、変域の考え方に慣れてもらいましょう。

一次関数の文章題の解き方を教えるポイント

文章題の攻略は次の2パターンです。

①文章題の言葉→直線の式（→グラフ）

②文章題の言葉＋グラフ→直線の式

ポイントは、ｘ・ｙをどうおいて、日本語の文章をどのように数式化していくか、です。

最初のうちは、解説の意味を読み解くところから始めてもよいでしょう。

以下、例題を挙げておきます。解説では、どのように考えているかまで書いていますので、お子さんに教える際の参考にしてください。

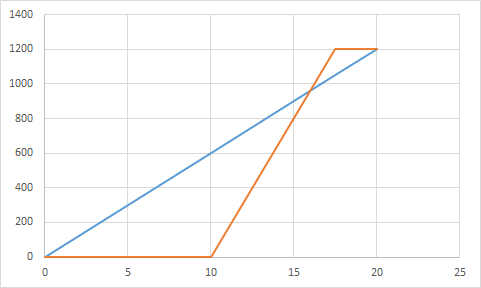
【解説】

〈例題１〉

一定の割合というのが、変化の割合ａを表していますので、毎分ａLの水が抜かれているとおきます。

また、水を抜いた時間をｘ分、水槽の水の量をｙLとして、ｙ＝ーａｘ＋１００とおけるかどうかがポイントです。

6分後に水槽の水は64Lになっているので、６４＝ー６ａ＋１００となり、ａ＝６です。

あとは、ｙ＝ー６ｘ＋１００にｘ＝１０を代入すればＯＫ。答えは、40Lです。

〈例題２〉

姉がAさんに追いついた地点は、Aさんの進む様子を表す一次関数のグラフと、姉が進む様子を表す一次関数のグラフとの交点だといえます。

Aさんの進む様子を表す直線の式を求めましょう。

グラフより、原点（０、０）を通るので、ｙ＝ａｘとおけます。

点（２０、１２００）を通ることから、ａ＝６０となるので、ｙ＝６０ｘ……①

次に、姉が進む様子を表す直線の式を求めましょう。

グラフより、点（１０、０）と点（１５、８００）を通ることから、ｘが５増加する間に、ｙは８００増加していることがわかります。

変化の割合ａは、８００÷５＝１６０なので、ｙ＝１６０ｘ＋ｂとおけます。

（ｘ、ｙ）＝（１０、０）を代入して０＝１６０・１０＋ｂより、ｂ＝ー１６００となるので、ｙ＝１６０ｘー１６００……②

①と②の交点では、①の（ｘ、ｙ）と②の（ｘ、ｙ）の値は同じになるはずです。

したがって、ｙ＝６０ｘ＝１６０ｘー１６００が成立します。

１６０ｘー１６００＝６０ｘ

移項すると、１６０ｘー６０ｘ＝１６００となり、１００ｘ＝１６００より、ｘ＝１６です。

これを①に代入すると、ｙ＝960となります。

以上より、姉がAさんに追いついたのは、Aさんが家を出発してから16分後で、家から960ｍの地点です。

概要が理解できれば問題演習を重ねよう

教えてもらっている状態で問題が解けたとしても、独力でできなければ意味がありません。分かった気になっているだけ、ということもあります。

思考力が問われる数学であっても、反復練習は非常に大事です。簡単な問題から標準レベルの問題まで、段階を踏んで解いていくようにしましょう。

解けた問題には○、解けなかった問題には△や×をつけ、2周目以降では△や×の問題を中心にやり直すようにしてください。

オススメの問題集は、『中学校3年間の数学が1冊でしっかりわかる問題集』（かんき出版）や『チャート式中学数学 シリーズ』（数研出版）です。

お子さんの理解が進まないパターン3選とその対処法

教えてもなかなか理解してもらえない

根気よく何度も例題レベルの問題を一緒に解いてください。

ヒントを出しながら解いてもらい、徐々にヒントの量を減らすというのも有効です。

一次関数の文章題では、解説の1行1行の意味を押さえることが大切です。

どのように日本語を数式化しているかを理解しましょう。

様々なパターンの問題がありますので、とにかく数をこなし、慣れることが大事です。

教えるとその場ではできるのに、お子さん一人で問題を解くと間違いが多発

このパターンは、さらに以下の2パターンに大別できます。

①問題演習が足りていない

→問題演習で基礎レベルから順番に解いていきましょう。

②教えられた時は分かった気になっている

→どこでつまずいているのかを分析、理解できていないポイントを再説明しましょう。その後、説明したポイントが理解できているかを測れる問題を演習できるとベストです。

変域をグラフ化することと、文章題における日本語を数式化すること。この二つが難所です。丁寧に学習を進めてあげてください。

教えようとすると、ちょっとした間違いを指摘しただけで機嫌が悪くなり、うまくいかない

思春期で親子関係が難しく、接し方にデリケートな配慮が必要な場合があります。

1つ指摘するときは1つ以上ほめることを意識しましょう。ほめる内容は、学習を着実に進められている点などにするのがオススメです。

そして大事なことは、「根気強く、粘り強く」です。保護者の方が不機嫌になったり、イライラしたりしないように心がけてください。

子どもに教えるというのは、なかなかにストレスが溜まる作業です。保護者の方の息抜きも必要でしょう。根を詰めてやりすぎると、保護者の方もお子さんもしんどくなってしまいます。

教えるのが大変……。成績低迷に悩む中高一貫校生なら、専門塾WAYSで92.9％が成績アップ！

最後に、お子さんが中高一貫校生で、成績低迷に悩んでいるのであれば、「中高一貫校専門 個別指導塾WAYS」をおすすめします。

• 思春期で親子関係が難しくなってきた
• 子どもの勉強を見る時間がなかなか取れない
• 勉強の内容が難しくなり、教えられなくなってきた

以上のように、家庭でのサポートが難しい場合にも、学習塾の活用は理にかなっています。

500校以上の指導ノウハウ＆9割以上の成績アップ実績

WAYSは、成績が低迷してしまっている中高一貫校生の、授業・定期テストのサポートに特化した、補習塾タイプの個別指導塾です。

一番の強みは、500校以上の中高一貫校生を指導してきたノウハウと、9割以上の塾生の成績を跳ね上げてきた実績です。

確認テストの実施や、生徒に問題を解説してもらうなどの指導スタイルで、塾生は確実に理解を深めていきます。